Jillian's Guide to Black Holes: Forming - Types - Outside - Inside - Finding - References - Websites
The Coordinate System
I will attempt to explain spacetime diagrams with the help of Lupin, my pet bird (shown to the right). I won't be able to explain every little mathematical detail about spacetime diagrams; but I will explain how to evaluate them visually. This way you can understand the spacetime diagrams on this page. I should warn you about the axes. This is not the standard x-y crosshair. For spacetime diagrams the y-axis (the vertical one) represents time. The x-axis (the horizontal one) represents space. This is a 1-1 diagram, which means there is only one time dimension (which we are used to) and one space dimension (which we are not).
We're used to living and moving in three spatial dimensions. What does 1D space look like? It's like living on a line: all you can do is go forward or go backward. That's it. No left, right, up, or down. That's what these spacetime diagrams describe, 1 time dimension and 1 space dimension. Why only 1? To represent two spatial dimensions would require a three dimensional graph, which are tough to draw. To represent three spatial dimensions would require a four dimensional graph, which would probably have to be some kind of animated thing and even more difficult to draw.
Walking through the parts of a spacetime diagram
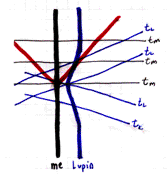There are black lines, red lines, and blue lines. Those thick vertical'ish lines are called worldlines. The black one describes what I'm doing and the blue one describes what my bird, Lupin, is doing. In this diagram Lupin sits still for a while, flies towards me, flies away from me and back to his previous position, and stays there. I just stay in one place. So, you know what those thick lines are, but what about the thin ones? Those are lines of simultaneity. Those are lines of constant time. You know, 1 second, 2 seconds, 3 seconds. Those red lines? They're light rays. Light rays are always drawn at 45°. Anything with matter cannot realistically have a worldline with a slope equal to or greater than 45° because matter cannot go the speed of light (and nothing can go faster than light).
So far things seem simple. Then again, maybe not. There are two sets of thin lines, mine and Lupin's. Things that are simultaneous are simultaneous, you say. Well...not quite. If you are standing still (which is tricky), your lines of simultaneity are horizontal. If you are moving your lines of simultaneity tilt. The angle between your worldline and a light ray is the same angle between the light ray and your line of simultaneity. The faster you go, the more those lines of simultaneity tilt from strictly horizontal. Confused? That's okay, here's an additional section on lines of simultaneity.
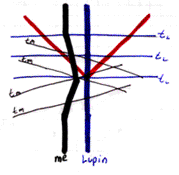The spacetime diagram to the right is the same event that just happened, except this one's drawn from Lupin's perspective. There is an important concept in drawing spacetime diagrams: the inertial reference frame. You'll notice that the same incident can be drawn differently, depending on what everything is drawn relative to. Which one of these two diagrams is the right one? Both. They are both accurate representations of what happened. In my eyes Lupin flew towards and then away from me. I thought I was standing still. In Lupin's eyes he was standing still and I moved towards and then away from him. Whoever the diagram is drawn with respect to must have a straight and vertical worldline.
