Gothos: Jillian's Guide to Black Holes

Gravity and the Eternal Black Hole

Great, we can do spacetime diagrams of moving objects even if they're accelerating. Still, what do we use to describe gravity? Hmm. Well, in 1959 two scientists (Pound and Rebke) proved that a gravitational field behaves just like acceleration. This is great, we know how to deal with acceleration! Are you ready? Then here's the spacetime diagram of a black hole:

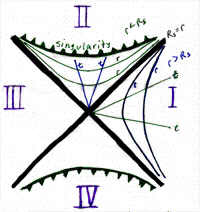
Region One

Actually, this is the diagram of an eternal black hole, one that always has been and always will be; but I will get to that later. Now, what are all the parts of the diagram? There are the light rays, the thick black lines at 45°. That's the event horizon. Those blue vertical'ish parabolas are our friends, the lines of constant distance. Why must the lines of constant distance be like parabolas and not straight lines? Well, to stay in one place in a gravitational field means that you must have an acceleration equal to the acceleration of gravity. Also, there are the green lines of simultaneity. We can recognize these parts from the diagram for an accelerated object. We understand region One.

Region Two

What about region Two? Well, it looks like the picture for constant time, except---time and space seem to have switched axes! What gives? This is what happens when you cross an event horizon: time and space flip axes. What does this mean? Well, light rays still travel at 45°. Unfortunately, once you cross the event horizon, you would have to travel with a slope of greater than 45° to recross it and get back into your universe. Okay, if you're stuck inside of the event horizon, what's that singularity thing? It seem to be everywhere; does that mean you eventually hit it? Well, kinda. Since time and space did a flip around, the singularity is not an actual spatial distance. It is, instead, a place in time. You will not hit the singularity after falling so many meters, but you will hit it after falling so many seconds. That takes care of region Two.

Region Three

Ah, region Three. What to do about that. The funny thing is, region Three looks just like region One, except it's on the other side of the black hole's event horizon. Hmm! It is a universe in its own right, but it is not our universe. We regretfully cannot travel there, for to do that we would have to travel faster than the speed of light to recross the event horizon. What about where the "two" event horizon's intersect? To travel that line would involve instantaneous transportation, which violates the whole matter-not-being-able-to-move-faster-than-the-speed-of-light concept. Travelers from the different universes could meet inside the event horizon, though, for the short time that they survive.

Region Four

I didn't mention region Four. It is much like region Two with two important differences. One: it happened infinitely in the past. Two: it appears to have repulsive gravity. It does in fact have repulsive gravity. The singularity in region Four is what astrophysicists like to call a white hole. People also call it the Big Bang. It is a time when matter is ejected violently from the singularity and shot away with the repulsive gravity. Region Four is rather speculative and only theoretical. Recall that I said this was a diagram for an eternal black hole? Well, most black holes are not eternal. They form, they exist, and Hawking would say that they also cease to exist. Here is the spacetime diagram for a mortal black hole:

A Mortal Black Hole

What's happening here? Well, that blue stuff is gas and dust. You can see that it is collapsing. When it collapses to its Schwarzschild Radius, an event horizon forms. There is a short time (we're talking nanoseconds) after the event horizon forms when objects falling in can encounter the gas. After that time all that is inside the black hole is curved spacetime. It's rather odd to think that a black hole is so strong, but there is nothing there that's doing anything.